Distintas Formas de Ecuacion de La Recta

Ecuación general de la recta.

Nos gustaría tener una forma de la ecuación de la recta que cubriera tanto a las rectas verticales como a
las que no lo son. Esta forma es la ecuación general de la recta y se obtiene pasando todos los términos de
la ecuación a un miembro de manera que este quede igualado a cero.
Ecuación general de la recta 3: Ax + By +C = 0 .
Recordemos que dos ecuaciones son equivalentes cuando obtenemos una a partir de la otra efectuando las
operaciones siguientes:
1. Sumar la misma cantidad (que puede ser una expresión algebraica) de ambos lados de una ecuación.
2. Multiplicar ambos lados de una ecuación por la misma cantidad distinta de cero.
Dos ecuaciones que son equivalentes representan el mismo lugar geométrico, en el caso de ecuaciones
lineales en dos variables, representan la misma recta.
Observa que la ecuación general de la recta no es única, ya que si multiplicamos la ecuación anterior por
una constante λ distinta de cero, obtenemos la ecuación;
λ Ax +λ By +λC = 0
que es de la misma forma que la anterior. Así, las tres ecuaciones siguientes son equivalentes y todas
están en la forma general;
3x -6y + 12 = 0,
x -2y + 4 = 0,
-x + 2y -4 = 0
y representan a la recta cuya ecuación pendiente-ordenada al origen es:
y = 2x + 2
45
y esta ecuación es equivalente a las anteriores, pues se obtiene a partir de cualquiera de las anteriores
utilizando sucesivamente las dos operaciones enunciadas anteriormente.

Ecuación principal de la recta

Esta es otra de las formas de representar la ecuación de la recta.

Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:

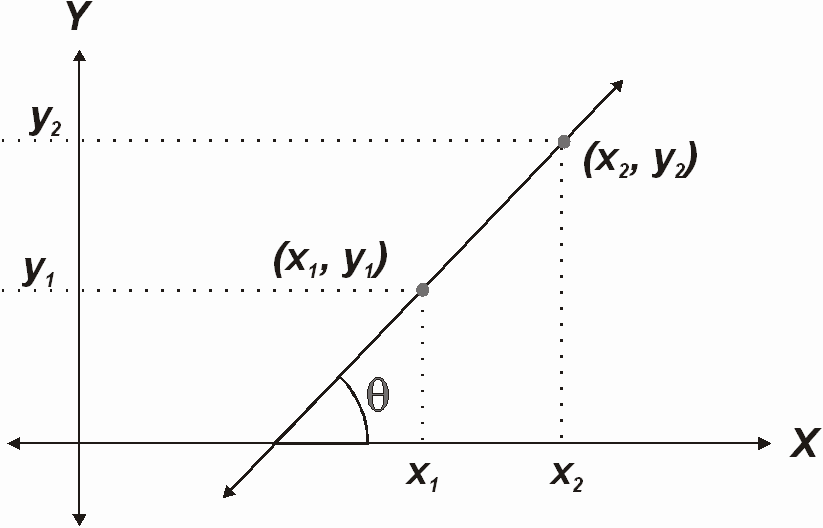
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa ey el valor de la ordenada.

(x, y) = (Abscisa , Ordenada)

Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.

Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.

Ejemplo: El punto (7, 2) (el 7 en la abscisa x y el 2 en la ordenada y) satisface la ecuación y = x – 5, ya que al reemplazar queda

2 = 7 – 5 lo que resulta verdadero.

Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce, que se obtiene con la fórmula

y = mx + n

Ecuación Punto-Pendiente

y-y1= m(x-x1) Esta ecuación se utiliza cuando deseamos obtener la ecuación de una recta si conocemos dos puntos de la recta o un punto y la pendiente

Determinacion de la ecuacion de la recta

Determinación de la ecuación de la recta.

Ecuación de la recta conociendo la pendiente y un punto de ella.

Como ya hemos visto antes las ecuaciones en dos variables representan lugares geométricos en el plano.

Empezaremos nuestro estudio de lugares geométricos con las rectas, que son los más sencillos.

Consideremos el problema de encontrar la ecuación de la recta no vertical que pasa por un punto
P(x1, y1) y tiene pendiente m.
Si Q(x, y) es cualquier otro punto de la recta, se debe satisfacer m= y2-y1 / x2- x1


Esta forma de la ecuación de la recta se llama ecuación punto-pendiente de la recta, ya que la obtuvimos
conociendo la pendiente y un punto de ella, y recíprocamente si vemos una ecuación de este tipo,
podemos saber por que punto pasa la recta y que pendiente tiene.

Condiciones de Paralelismo y Perpendicular

Condiciones de Paralelismo y Perpendicularidad

Paralelismo

He aquí dos criterios para determinar si dos rectas son paralelas:

Dos rectas son paralelas si tienen la misma dirección y ésto ocurre cuando sus vectores de dirección son iguales o proporcionales.

Proposición

---

Dos rectas son paralelas si y sólo si sus pendientes coinciden m= m'

Vimos que la pendiente de una recta coincide con la tangente del ángulo que forma con el eje de abscisas, por tanto, si dos rectas tienen la misma pendiente, las tangentes de los ángulos que forman, serán iguales. Ahora, si las tangentes de dos ángulos son iguales, los ángulos o son iguales o difieren en 180º. En ambos casos las rectas tienen la misma inclinación.

Y recíprocamente, si dos rectas son paralelas, los ángulos que forman con el eje de abscisas son iguales y, por tanto, sus tangentes. Luego las pendientes son también iguales.

Perpendicularidad

He aquí dos criterios para determinar si dos rectas son perpendiculares:

Dos rectas son perpendiculares si sus vectores de dirección son ortogonales, o lo que es lo mismo, si el producto escalar de sus vectores de dirección es cero. Traduciendo ésto a coordenadas: Dos rectas con vectores de dirección: (d1,d2) y (-d2,d1)

La relación de perpendicularidad se puede dar entre:

• Rectas: dos rectas coplanarias son perpendiculares cuando, al cortarse, dividen al plano en cuatro regiones iguales, cada una de los cuales es un ángulo recto. Al punto de intersección de dos rectas perpendiculares se le llama pie de cada una de ellas en la otra.
  • Semirrectas: dos semirrectas son perpendiculares, cuando conforman ángulos rectos teniendo o no el mismo punto de origen.

La Linea Recta

Introducción       12/Octubre/2012

Escuela : Cetis 71

Alumno: Roberto Angel Maldonado Juarez

Materia: Geometría Analítica

Maestra: Martha Reyna Martinez

Grupo: 3K                   Especialidad: Contabilidad

Tema de Investigación: "La Linea Recta" 

La línea recta.

Todos tenemos la idea intuitiva de lo que es una recta. Las propiedades fundamentales de la recta, de
acuerdo a los Axiomas de Euclides, son: Por dos puntos distintos pasa una y sólo una recta. Dos rectas
distintas se cortan en un sólo punto o son paralelas.

Ángulo de inclinación

Sea 1 una recta no paralela al eje x y que lo intersecta en el punto A.
La dirección de la recta en relación con los ejes coordenados puede indicarse si se conoce el ángulo θ <
180° que se obtiene al girar la semirrecta AX en sentido contrario alas manecillas del reloj hasta coincidir
con la recta 1. Por lo tanto, este ángulo (θ) se denomina inclinación de la recta 1.

Pendiente de Una Recta

Si la recta es vertical, todos los puntos de la recta tienen la misma primera coordenada, entonces el

denominador de la expresión anterior vale cero y por lo tanto, no puede evaluarse m, así que las rectas

verticales no tienen pendiente.

0bservaciones:

o La pendiente es positiva cuando la recta esta inclinada hacia la derecha.

o La pendiente es cero cuando la recta es horizontal.

o La pendiente es negativa cuando la recta esta inclinada hacia la izquierda.

o Conforme el valor absoluto de la pendiente es mayor, la recta esta mas inclinada.

o Una recta vertical no tiene pendiente.La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas. Se denota con la letra m.

Pendiente dado el angulo m= tg α
Pendiente dado dos puntos m= y₂ - y₁ / x₂ –x₁